728x90
반응형

| Rank : 6 , 점수: 310 , 출제수: 16문제 , 논술 : 10문제 , 약술: 6문제 |
| 20-121-1-3 | AHP(Analytical Hierarchical Process)의 쌍대비교(Pair-wise Comparison) |
| 문) | AHP(Analytical Hierarchical Process)의 쌍대비교(Pair-wise Comparison) | ||
| 문제별 구성요소들은 그들이 내포하고 있는 특징별로 상대적인 영향 측면에서 | |||
| 한쌍씩 비교되는데, 즉 각 평가요소를 1대1로 비교하여 상대적 중요도를 결정 | |||
| 하게 된다. 두 요소를 비교할 경우에 비교하는 방법은 A와 B중에 어느 것이 더 | |||
| 중요한가(심각한가)? 라고 질문하게 되는데, 그 심각성의 정도를 비교하는 데 | |||
| 사용되는 쌍체비교의 척도는 일반적으로 다음과 같이 1에서 9까지 사이의 | |||
| 점수를 사용하게 된다. | |||
| 20-121-1-11 | 선형계획법이 주로 응용되는 분야 5가지 |
| 문) | 선형계획법이 주로 응용되는 분야 5가지 | ||
| 선형계획법(linear programming)이란 최적화 문제의 일종으로 주어진 선형 | |||
| 조건들을 만족시키면서 선형인 목적 함수를 최적화하는 문제이다. | |||
| 선형계획법 응용되는 분야 | |||
| 1. 마케팅 : 광고매체 선정, 유통단지 입지선정 | |||
| 2. 재무관리 : 포트폴리오 구성, 자금운용계획, 자금조달 방법 결정 | |||
| 3. 인사관리 : 인력수급계획, 교대근무계획 | |||
| 4. 생산관리 : 생산계획 및 재고관리 문제, 생산제품 배합 문제, 생산 및 배분 | |||
| 문제, 식 | |||
| 단 문제, 원료혼합 문제 |
| 20-121-2-5 | 부품 회사는 2개 제품을 생산하기 위하여 공장1, 공장2, 공장3에서 주어진 시간만큼 |
| 가공시간이 필요하다. 제품1과 제품2의 개당 이익은 각각 30만원과 50만원이고, 주당 | |
| 총이익을 최대화하려 한다. 3개 공장의 주당 이용가능시간은 각각 6, 14, 18(시간/주) | |
| 이다. 제품당 필요한 가공시간은 아래와 같고 가공순서는 고려하지 않는다. 다음 물음에 | |
| 답하시오. | |
 |
|
| 1) 선형계획문제로 정식화(대수식)하시오. | |
| 2) 1)항을 그래프로 도식화하고 최적해를 구하시오. | |
| 3) 공장2와 공장3의 이용가능시간을 증가시키려 할 때 그래프를 활용한 민감도분석을 | |
| 이용하여 공장2와 공장3의 1시간의 가치를 계산하시오. |
| 문) | 부품 회사는 2개 제품을 생산하기 위하여 공장1, 공장2, 공장3에서 주어진 | ||
| 시간만큼 가공시간이 필요하다. 제품1과 제품2의 개당 이익은 각각 30만원과 | |||
| 50만원이고, 주당 총이익을 최대화하려 한다. 3개 공장의 주당 이용가능시간 | |||
| 은 각각 6, 14, 18(시간/주)이다. 제품당 필요한 가공시간은 아래와 같고 가공 | |||
| 순서는 고려하지 않는다. 다음 물음에 답하시오. | |||
 |
|||
| 1) 선형계획문제로 정식화(대수식)하시오. | |||
| 2) 1)항을 그래프로 도식화하고 최적해를 구하시오. | |||
| 3) 공장2와 공장3의 이용가능시간을 증가시키려 할 때 그래프를 활용한 민감 | |||
| 도분석을 이용하여 공장2와 공장3의 1시간의 가치를 계산하시오. | |||
| 1) | (1) 의사결정변수 | ||
| 제품 1 : A의 생산량 | |||
| 제품 2 : B의 생산량 | |||
| (2) 목적함수 | |||
| Max Z=30A+50B | |||
| (3) 제약조건 | |||
| 1A+0B≤6 | |||
| 0A+2B≤14 | |||
| 번호 | |||
| 2A+2B≤18 | |||
| (4) 비음조건 | |||
| A, B ≥ 0 | |||
| 2) | 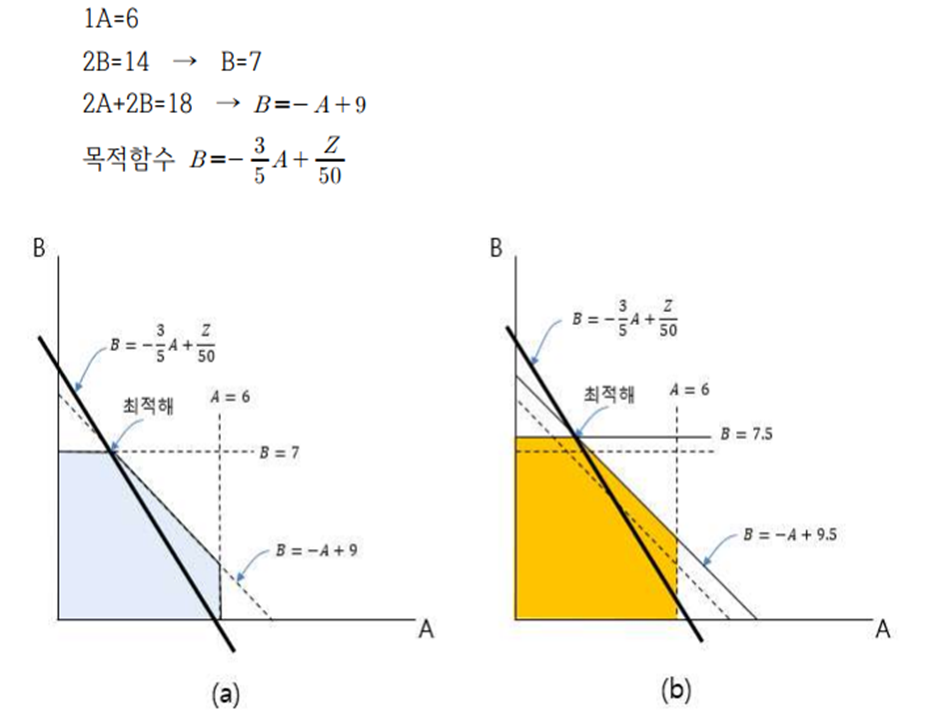 |
||
| 최적해 A=2(개), B=7(개), Z=60+350=410(만원) | |||
| 3) | 2B=14 → 2B=15 → B=7.5 | ||
| 2A+2B=18 → 2A+2B=19 → B = -A + 9.5 | |||
| 최적해 A=2(개), B=7.5(개), Z=60+375=435(만원) | |||
| 따라서 공장2와 공장3의 이용가능시간을 1시간 증가함으로써, 제품 1에 대한 | |||
| 생산량은 변함이 없으나, 제품2에 생산량 증가로 이어짐으로써 1시간의 | |||
| 가치는 주당 이익 25만원(410만원→435만원)의 증대로 이어지고 있다는 | |||
| 분석이 가능하다. | |||
| 18-115-1-2 | ANP(Analytic Network Process) 기법 |
| 문) | ANP(Analytic Network Process) 기법 | ||
| AHP에 기초를 둔 시스템 분석, 통합 및 조정을 위한 방법으로 요소 간의 | |||
| 비선형 관계를 모델화하는 복잡한 의사결정을 다룰 수 있다. ANP는 목표, | |||
| 기준, 대안 상호 간의 종속성이나 피드백을 포함하는 네트워크 구조의 의사 | |||
| 결정 시스템으로 AHP를 확장한 새로운 방식이며, 이를 해결하는 방법으로 | |||
| 대행렬(Supermatrix)을 이용한다. 이를 구성하는 의사결정 문제가 군집 내, | |||
| 군집 간의 교호작용이나 피드백을 포함할 수 있다는 장점을 가진 기법이다. | |||
 |
|||
| 18-115-4-5 | S전자는 오송지역에 거점창고를 설치하려고 한다. 거점창고 운영 시 시장성이 좋으면 |
| 100억 원의 이익이 발생하고, 시장성이 좋지 않으면 20억 원의 손실이 발생한다. 이러한 | |
| 위험을 줄이기 위해 10억 원을 지불하고 전문조사기관에 사업성분석 용역을 주는 경우 | |
| 분석이 잘 될 확률은 70%이고, 잘 되지 않을 확률은 30%이다. 또한 분석이 잘 된 경우에 | |
| 있어 시장성이 좋을 확률은 80%, 나쁠 확률은 20%이며, 분석이 잘 되지 않은 경우에 | |
| 있어 시장성이 좋을 확률은 10%, 나쁠 확률은 90%이다. 한편, 사업성 분석을 하지 않을 | |
| 경우, 시장성이 좋을 확률과 나쁠 확률은 각각 50%이다. | |
| 다음은 이를 바탕으로 의사결정모형의 구성요소인 대안과 상황을 정리한 것이다. | |
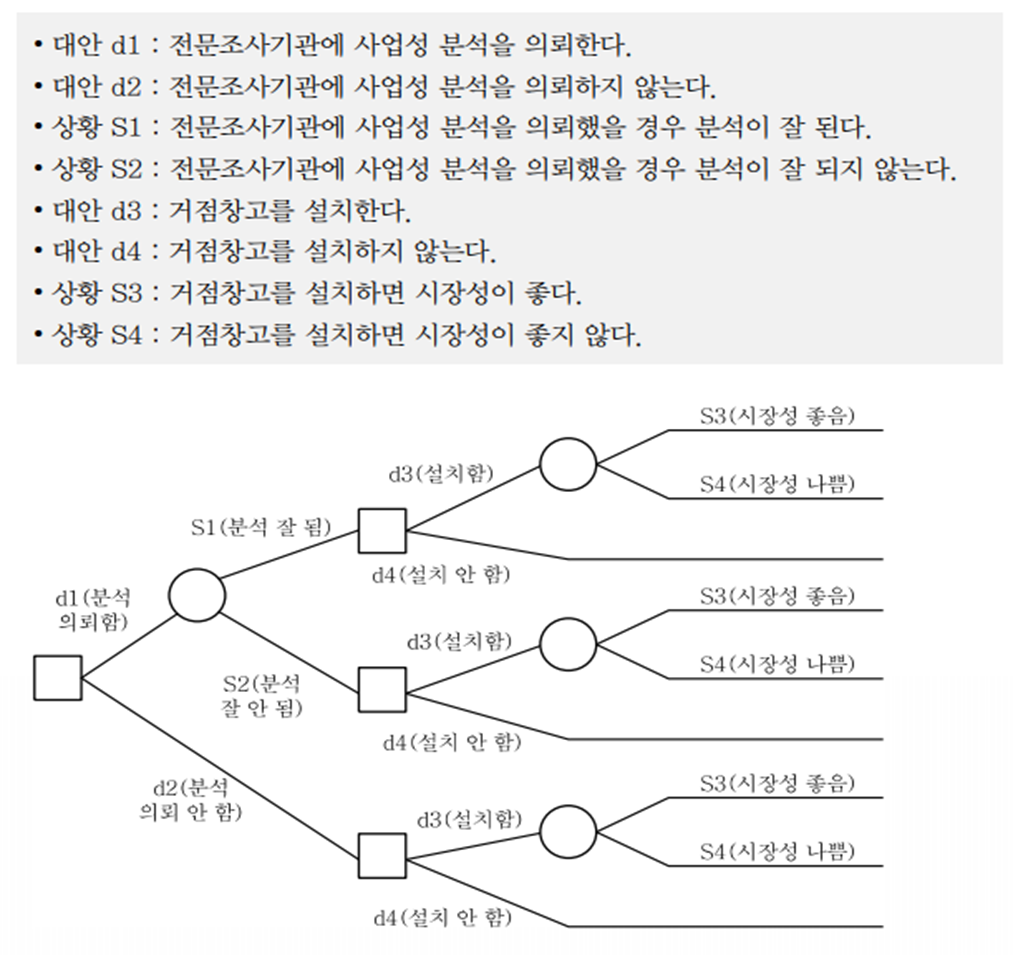 |
|
| (1) 분석의뢰를 하는 경우의 EMV(d3/S1)와 EMV(d4/S1)를 비교하시오.(단, EMV는 Expected | |
| Monetary Value이다.) | |
| (2) 분석의뢰를 하는 경우의 EMV(d3/S2)와 EMV(d4/S2)를 비교하시오. | |
| (3) 분석의뢰를 하지 않는 경우의 EMV(d3)와 EMV(d4)를 비교하시오. | |
| (4) EMV(d1)와 EMV(d2)를 비교하시오. | |
| (5) 앞의 결과를 고려하여 종합적 의사결정을 수행하시오. |
| 문) | S전자는 오송지역에 거점창고를 설치하려고 한다. 거점창고 운영 시 시장성이 | ||
| 좋으면 100억 원의 이익이 발생하고, 시장성이 좋지 않으면 20억 원의 손실이 | |||
| 발생한다. 이러한 위험을 줄이기 위해 10억 원을 지불하고 전문조사기관에 | |||
| 사업성분석 용역을 주는 경우 분석이 잘 될 확률은 70%이고, 잘 되지 않을 | |||
| 확률은 30%이다. 또한 분석이 잘 된 경우에 있어 시장성이 좋을 확률은 80%, | |||
| 나쁠 확률은 20%이며, 분석이 잘 되지 않은 경우에 있어 시장성이 좋을 확률은 10%, 나쁠 | |||
| 확률은 90%이다. 한편, 사업성 분석을 하지 않을경우, 시장성이 좋을 확률과 | |||
| 나쁠 확률은 각각 50%이다. 다음은 이를 바탕으로 의사결정모형의 구성요소 | |||
 |
|||
| 번호 | |||
| (1) 분석의뢰를 하는 경우의 EMV(d3/S1)와 EMV(d4/S1)를 비교하시오.(단, | |||
| EMV는 Expected Monetary Value이다.) | |||
| (2) 분석의뢰를 하는 경우의 EMV(d3/S2)와 EMV(d4/S2)를 비교하시오. | |||
| (3) 분석의뢰를 하지 않는 경우의 EMV(d3)와 EMV(d4)를 비교하시오. | |||
| (4) EMV(d1)와 EMV(d2)를 비교하시오. | |||
| (5) 앞의 결과를 고려하여 종합적 의사결정을 수행하시오. | |||
| (1) EMV(d3/S1):(100억 원×0.8)+(-20억 원×0.2)=76억 원 (결정) | |||
| EMV(d4/S1):0 | |||
| (2) EMV(d3/S2):(100억 원×0.1)+(-20억 원×0.9)=-8억 원 | |||
| EMV(d4/S2):0 (결정) | |||
| (3) EMV(d3):(100억 원×0.5)+(-20억 원×0.5)=40억 원 (결정) | |||
| EMV(d4):0 | |||
| (4) EMV(d1):(76억 원×0.7)+(0억 원×0.3)=53.2억 원-10억 원=43.2억 원 (최종결정) | |||
| EMV(d2):40억 원 | |||
| (5) 오송지역에 거점창고를 설치하는 의사결정을 위해서 10억 원의 분석비용을 지불 | |||
| 하여 분석할 결과에 따라 설치를 고려하는 것이 유리하다고 판단할 수 있다. | |||
| 17-112-3-5 | 생산시스템에 적용되는 시뮬레이션의 의의 및 장단점에 대하여 각각 설명하시오. |
| 문) | 생산시스템에 적용되는 시뮬레이션의 의의 및 장단점에 대하여 각각 | ||
| 설명하시오. | |||
| 1. | 정의 | ||
| 시뮬레이션이란 최적해를 도출하는 기법이라기보다는 어떤 실제 현상을 모형 | |||
| 화하여 제작한 후, 그 모형에 대한 실험을 수행함으로써, 관계되는 결과치를 | |||
| 도출하고 이를 실제 현상에 적용하기 위한 방법 이다. | |||
| 2. | 시뮬레이션을 사용하는 이유는 실제 상황에 대한 실험이 비실용적이거나 | ||
| 불가능할 경우, 수학적인 표현이나 모델의 해를 제시하기에 실제 상황이 | |||
| 너무 복잡할 경우에 사용하게 된다. | |||
| 3. | 장점 | ||
| 1) | 다른 경영과학기법으로 다룰 수 없는 복잡하고 동적인 현상을 모형화한다. | ||
| 2) | 다른 방법으로는 불가능하거나 실행하지 못할 것 같은 실험을 가능하게 한다. | ||
| 3) | 시뮬레이션을 실행함으로써 경영과학자는 시스템과 서로 다른 변수들의 상대 | ||
| 적인 중요성에 대한 귀중한 통찰력을 얻게 된다. | |||
| 4) | 시뮬레이션은 실제 시간을 압축하도록 한다. | ||
| 5) | 시뮬레이션의 기본 개념을 이해하기 위해서는 복잡한 수학적 지식이 없어도 | ||
| 되며, 결과적으로 경영진들은 시뮬레이션을 의사결정도구로서 더 많이 | |||
| 2쪽 | |||
| 번호 | |||
| 사용하고자 한다. | |||
| 4. | 단점 | ||
| 1) | 시뮬레이션은 최적해 기법이 아니다. 전형적인 하나의 훌륭한, 그러나 최선이 | ||
| 보장된 것이 아닌 해법을 찾기 위해 실험된다. | |||
| 2) | 시뮬레이션은 문제를 해결하는 데 매우 비싼 방법이다. 시뮬레이션 모형을 | ||
| 만들고, 타당성을 조사하는 것 이외에도 컴퓨터 시뮬레이션을 사용하는 | |||
| 실험은 많은 비용을 수반할 수도 있다. | |||
| 3) | 시뮬레이션의 본질적 특성 때문에 표본 오류가 확률적 시뮬레이션 모형들로 | ||
| 부터 나온 모든 결과에서 존재한다. | |||
| 4) | 실제 시뮬레이션 프로그램을 작성할 수 있는 능력을 가진 사람이 전체적인 | ||
| 시뮬레이션 연구를 수행할 능력이 없기 때문에 시뮬레이션이 종종 잘못 | |||
| 사용되고 있다. | |||
| 5) | 가장 심각한 문제로 시뮬레이션이 해결책에 대한 평가 도구로 쓰인다는 | ||
| 점으로 문제해결안을 생성하지 않는다는 것이다. | |||
| 15-106-2-1 | 의사결정과 관련한 다음 각 물음에 답하시오. |
| (1) 확실성하의 의사결정, 불확실성하의 의사결정, 위험하의 의사결정에 대하여 각각 설명하시오 | |
| (2) A기업은 콘도미니엄 건설을 위해 소규모, 중규모, 대규모 등 3가지 대안을 고려하고 있다. | |
| 다음 표와 같이 수요에 따른 이익이 예상될 때 1) Laplace 기준, 2) Wald 기준, 3) Maximax 기준, 4) Savage 기준, 5) Hurwicz 기준(단, =0.4)에 의하여 각각 최선의 대안을 결정하시오. | |
 |
| 문) | 의사결정과 관련한 다음 각 물음에 답하시오. | ||
| (1) 확실성하의 의사결정, 불확실성하의 의사결정, 위험하의 의사결정에 | |||
| 대하여 각각 설명하시오 | |||
| (2) A기업은 콘도미니엄 건설을 위해 소규모, 중규모, 대규모 등 3가지 대안을 | |||
| 고려하고 있다. | |||
| 다음 표와 같이 수요에 따른 이익이 예상될 때 1) Laplace 기준, 2) Wald 기준, | |||
| 3) Maximax 기준, 4) Savage 기준, 5) Hurwicz 기준(단, =0.4)에 의하여 | |||
| 최선의 대안을 각각정하시오. 결정하시오. | |||
 |
|||
| (1) 1) 확실성하의 의사결정 | |||
| 대안을 선택할 때 어떠한 상황이 발생할 것인지를 확실하게 알고 있는 경우 | |||
| (2) A기업은 콘도미니엄 건설을 위해 소규모, 중규모, 대규모 등 3가지 대안을 고려 | |||
| 하고 있다. 다음 표와 같이 수요에 따른 이익이 예상될 때 1) Laplace 기준, | |||
| 2) Wald 기준, 3) Maximax 기준, 4) Savage 기준, 5) Hurwicz 기준(단, ∝=0.4) | |||
| 에 의하여 각각 최선의 대안을 결정하시오. | |||
| (1) 1) 확실성하의 의사결정 | |||
| 대안을 선택할 때 어떠한 상황이 발생할 것인지를 확실하게 알고 있는 경우 | |||
| 2쪽 | |||
| 번호 | |||
| 2) 불확실성하의 의사결정 | |||
| 대안을 선택할 때 상황발생 확률을 전혀 모르는 경우 | |||
| 3) 위험하의 의사결정 | |||
| 대안을 선택할 때 상황 발생 여부를 확률적으로 알고 있는 경우 | |||
| 4) 상충하의 의사결정 | |||
| 서로 상충적인 이해관계를 가진 의사결정자들이 상대방에 대응하여 의사결정 | |||
| 을 하게 되는 경우 이를 게임모형(Game Mode)이라 한다. | |||
 |
|||
 |
|||
 |
|||
| 14-103-1-6 | 불확실성하의 의사결정법 중 Laplace기준에 대하여 다음의 자료를 이용하여 설명하시오 |
 |
| 문) | 불확실성하의 의사결정법 중 Laplace기준에 대하여 다음의 자료를 이용하여 | ||
| 설명하시오 | |||
 |
|||
| 1. |  |
||
| 14-103-2-3 | 대기행렬시스템에 대한 다음 각 물음에 답하시오. |
| (1) M/M/1 모형을 설명하고 이 모형이 성립하기 위한 가정 3가지를 설명하시오. | |
| (2) 홍길동은 혼자 이발소를 운영 중이다. 근무시간 10시간 동안 (식사시간이나 휴식시간은 | |
| 빈 시간을 활용하여 해결하므로 없다고 가정한다.) 일일 평균 고객 수는 40명이고 한 명당 이발 | |
| 시간은 평균 10분이다. 이 이발소가 M/M/1 조건을 만족하고 있을 때, 도착률(), 서비스율(), | |
| 시스템 내의 평균 고객 수(LS:Length in System)를 계산하시오. |
| 문) | 대기행렬시스템에 대한 다음 각 물음에 답하시오. | ||
| (1) M/M/1 모형을 설명하고 이 모형이 성립하기 위한 가정 3가지를 설명하시오. | |||
| (2) 홍길동은 혼자 이발소를 운영 중이다. 근무시간 10시간 동안 (식사시간이나 | |||
| 휴식시간은 빈 시간을 활용하여 해결하므로 없다고 가정한다.) 일일 평균 | |||
| 고객 수는 40명이고 한 명당 이발 시간은 평균 10분이다. 이 이발소가 M/M/1 | |||
| 조건을 만족하고 있을 때, 도착률(), 서비스율(), | |||
| 시스템 내의 평균 고객 수(LS:Length in System)를 계산하시오. | |||
| (1) (1) M:고객의 도착은 푸아송분포로 도착 | |||
| (2) M:서비스 시간이 지수분포 | |||
| (3) 1:서비스 시설이 하나이다. | |||
| (2) (1) 도착율():단위시간당 도착하는 고객 수 | |||
 |
|||
| (2) 서비스율() | |||
 |
|||
| (3) 시스템 내의 평균 고객 수 | |||
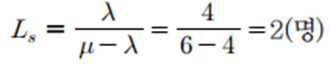 |
|||
| 14-103-4-2 | 등산용 텐트와 그늘막을 생산·판매하고 있는 고구려주식회사는 현재의 생산능력범위 | |
| 내에서 이익을 최대로 올릴 수 있는 텐트와 그늘막의 생산량을 각각 결정하려고 한다. | ||
| 이들 제품은 인발, 후가공, 조립의 3공정을 순차적으로 거쳐 제작되는데(단, 그늘막은 | ||
| 후가공을 하지 않는다.) 소요시간은 아래의 표와 같다. 그리고 각 공정별 월간 최대작업능 | ||
| 력은 인발 2,400시간, 후가공 1,500시간, 조립 2,700시간으로 이를 초과하여 작업할 | ||
| 수는 없다. 그리고 제품의 단위당 판매이익은 텐트 20,000원, 그늘막 10,000원이다. | ||
 |
||
| (1) 도시법(Graphic Solution Method)과 심플렉스 해법(Simplex Solution Method)의 장단점 | ||
| 을 비교하여 설명하시오. | ||
| (2) 선형계획모델을 설계하고, 도시법을 사용하여 최적해를 구하시오. |
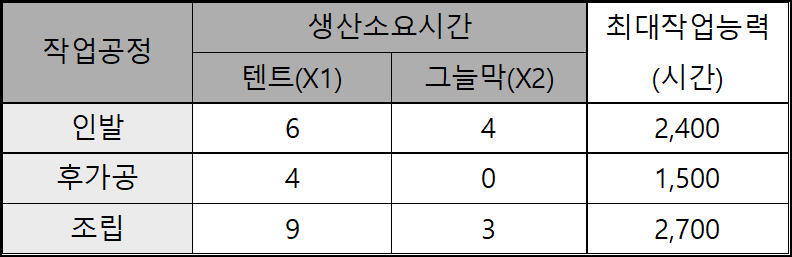
| 문) | 등산용 텐트와 그늘막을 생산·판매하고 있는 고구려주식회사는 현재의 생산 | ||
| 능력범위 내에서 이익을 최대로 올릴 수 있는 텐트와 그늘막의 생산량을 각각 | |||
| 결정하려고 한다. 이들 제품은 인발, 후가공, 조립의 3공정을 순차적으로 거쳐 | |||
| 제작되는데(단, 그늘막은 후가공을 하지 않는다.) 소요시간은 아래의 표와 | |||
| 같다. 그리고 각 공정별 월간 최대 작업능력은 인발 2,400시간, 후가공 1,500 | |||
| 시간, 조립 2,700시간으로 이를 초과하여 작업할 수는 없다. 그리고 제품의 | |||
| 단위당 판매이익은 텐트 20,000원, 그늘막 10,000원이다. | |||
 |
|||
| (1) 도시법(Graphic Solution Method)과 심플렉스 해법(Simplex Solution | |||
| Method)의 장단점을 비교하여 설명하시오. | |||
| (2) 선형계획모델을 설계하고, 도시법을 사용하여 최적해를 구하시오. | |||
| (1) 선형계획법이란 주어진 목적을 달성하기 위하여 어떻게 제한된 자원을 합리적으로 | |||
| 배분하느냐에 대한 의사결정 문제를 해결하기 위하여 개발된 수리적 기법 | |||
| 이다. | |||
| 선형계획법은 1차식으로 나타낼 수 있는 여러 가지 제약조건하에서 1차 방정 | |||
| 식으로 된 목적함수의 최대화 혹은 최소화(예를 들면, 이익의 최대화 혹은 | |||
| 2쪽 | |||
| 번호 | |||
| 비용의 최소화)를 달성할 수 있도록 자원을 배분하는 기법이다. | |||
| 1. 도시법 | |||
| 기하학적으로 그래프에 의해서 최적해를 구하는 이 도시법은 선형계획법 | |||
| 가운데 가장 간단한 방법이다. 그래서 이 방법은 선형계획모델의 일반구조를 | |||
| 설명하는 데 흔히 사용된다. 도시법은 그 작성이 용이하며 문제의 제약조건과 | |||
| 목적함수의 선형성등의 개념을 정확히 이해할수 있다는 장점이 있다. | |||
| 그렇지만 도표의 좌표를 읽어서 해를 구하므로 아주 정확하지는 못하며, | |||
| 변수가 3개 이상일 때는 최적해를 구하기 곤란하다는 결점이 있다. | |||
| 2. 심플렉스법 | |||
| 반복적 연산과정을 통하여 최적해를 찾는 방법으로, 선형계획법(LP)의 최적해 | |||
| 는 반드시 실행 가능영역의 꼭짓점이거나 꼭짓점을 포함한다는 점을 이용하 | |||
| 여, 실행가능영역의 꼭짓점을 옮겨가며 해를 개선해 나감으로써 최적해를 찾게 | |||
| 된다. 이때 실행가능영역상의 꼭짓점을 실행가능 기저해라 한다. | |||
| (2) 선형계획모델 설계 | |||
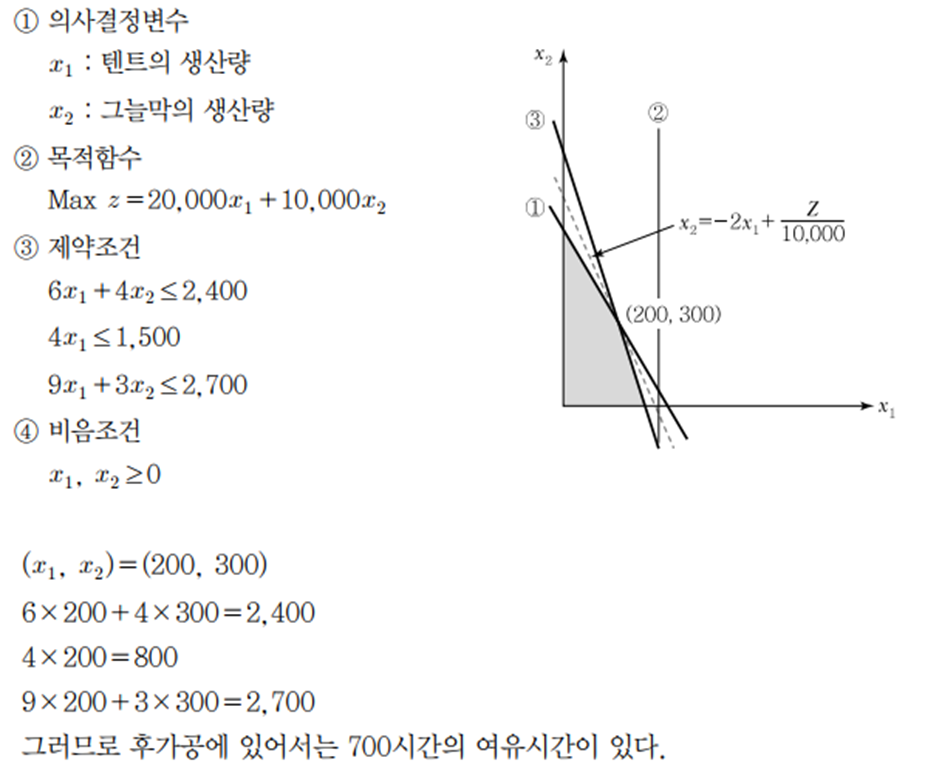 |
|||
| 13-100-1-6 | 성과 평가도구로서의 DEA(Data Envelopment Analysis) |
| 문) | 성과 평가도구로서의 DEA(Data Envelopment Analysis) | ||
| 1. | DEA(Data Envelopment Analysis, 자료포괄분석)는 1978년 Charnes, Cooper, | ||
| Rhodes에 의해 처음으로 제안되었으며, OR/M(Operations Research/ | |||
| Management, 운용과학/경영)에서 가장 널리 활용되는 방법 중 하나이다. | |||
| 2. | DEA의 가장 큰 특징은 ‘과제 중심적 접근’과 ‘중요한 과제에 초점’을 맞추어 | ||
| DMU(Decision Making Units, 의사결정 단위)의 성과를 평가한다는 점이다. |
| 13-100-2-1 | 불확실한 상황에서의 의사결정기준으로 Wald기준, Savage기준 등이 사용되고 있다. |
| 다음 각 물음에 답하시오. | |
| (1) 불확실한 상황에 대하여 설명하시오. | |
| (2) Wald기준과 Savage기준에 대하여 설명하시오, | |
| (3) A제품은 통상 장기계약(2~3년 이상), 단기계약(1년), 1회 계약의 세 가지 형태로 공급되고 있으며, | |
| 그 이익은 계약기간 동안의 시장경기에 따라 달라진다. 경기에 따른 계약형태별 이익의 경향이 다음 | |
| 표와 같을 때 Wald기준, Savage기준에 의한 각각 최선의 계약형태를 결정하시오. | |
 |
| 문) | 불확실한 상황에서의 의사결정기준으로 Wald기준, Savage기준 등이 사용되고 | ||
| 있다. 다음 각 물음에 답하시오. | |||
| (1) 불확실한 상황에 대하여 설명하시오. | |||
| (2) Wald기준과 Savage기준에 대하여 설명하시오, | |||
| (3) A제품은 통상 장기계약(2~3년 이상), 단기계약(1년), 1회 계약의 세 가지 형 | |||
| 태로 공급되고 있으며, 그 이익은 계약기간 동안의 시장경기에 따라 달라진다. | |||
| 경기에 따른 계약형태별 이익의 경향이 다음 표와 같을 때 Wald기준, Savage | |||
| 기준에 의한 각각 최선의 계약형태를 결정 하시오. | |||
 |
|||
| (1) 대안을 선택할 때 상황발생 확률을 전혀 모르는 경우 | |||
| (2) 1. Wald기준 | |||
| Maximin, 최대최소기준, 비관적 성향의 의사결정 대안들의 최솟값 중 가장 | |||
| 큰 값을 대안으로 결정 | |||
| 2. Savage기준 | |||
| 1) Minimax, 최소최대 후회기준, 보수적인 입장의 의사결정기준, 최대후회 | |||
| (기회손실) 중 최소인 대안선택 | |||
| 2) 상황별 기회손실을 산출하고 대안별로 기회손실이 가장 큰 값 중 가장 작은 | |||
| 기회손실 값을 갖는 대안을 결정 | |||
| 2쪽 | |||
| 번호 | |||
| (3) 1. Wald기준 | |||
 |
|||
| * 장기계약을 최적대안으로 결정한다. | |||
| 2. Savage기준 | |||
 |
|||
| * 1회 계약을 최적대안으로 결정한다. | |||
| 12-97-1-3 | 계층분석과정인 AHP(Analytic Hierarchy Process)의 정의와 기본적인 공리 4가지를 설명하시오. |
| 문) | 계층분석과정인 AHP(Analytic Hierarchy Process)의 정의와 기본적인 공리 | ||
| 4가지를 설명하시오. | |||
| 1. | 정의 | ||
| 1) | AHP는 Analytic Hierarch Process의 약어로 계층분석과정 또는 계층분석방법 | ||
| 이라고 불린다. AHP는 의사결정의 계층구조를 구성하고 있는 요소 간의 쌍대 | |||
| 비교를 통해 평가자의 지식, 경험 및 직관을 포착하는 의사결정방법론 중 하나 | |||
| 이다. 즉, 의사결정의 전 과정을 여러 단계로 나눈 후 이를 단계별로분석 해결 | |||
| 함으로써 최종적인 의사결정에 이르는 방법이라고 할 수 있다. | |||
| 2) | AHP는 다수의 대안에 대하여 다면적인 평가기준과 다수 주체에 의한 의사 | ||
| 결정을 위해 설계된 방법이다. 의사결정자의 직관적, 합리적 또는 비합리적 | |||
| 판단을 근거로 정량적인 요소와 정성적인 요소를 동시에 고려함으로써 의사 | |||
| 결정문제의 해결을 위한 포괄적인 틀을 제공해준다. | |||
| 2. | 기본적인 공리 4가지 | ||
| 1) | 상호 비교(Reciprocal Comparison) | ||
| 의사결정자의 두 대상에대한 상호 비교가반드시 가능해야하며중요성의 정도 | |||
| 를 나타낼수 있어야한다. 이 중요성의 정도는 반드시 역 조건을 성립시켜야 | |||
| 한다. 즉, A가 B보다 x배 중요하다면 B는 A보다 1/x배 중요시되어야 한다. | |||
| 2쪽 | |||
| 번호 | |||
| 2) | 동질성(Homogeneity) | ||
| 중요성의 정도는 한정된 범위 내의 정해진 척도를 통해 표현되어야 한다. | |||
| 즉, 비교대상 간에는 비교 가능한 일정한 범위를 갖는 기준들이 존재해야 | |||
| 한다. | |||
| 3) | 독립성(Independence) | ||
| 상대적인 중요도를 평가하는 동일 수준의 요인들은 특성이나 내용 측면에서 | |||
| 서로 관련성이 없어야 한다. | |||
| 4) | 기대성(Expectation) | ||
| 계층구조는 의사결정에 필요한 모든 사항들을 완전하게 포함하는 것으로 가정 | |||
| 한다. 즉, 의사결정자들의 합리적 기대에 부합하는 와전한 계층 구조를 가지고 | |||
| 있어야 하는 것이다. 반면에 수준의 수가 많아 계층 구조가 깊으면 계산상의 | |||
| 복잡성을 유발시키므로 일반적으로는 3~7수준으로 계층을 형성한다. | |||
| 12-97-2-5 | A와 B의 2가지 제품을 생산하고 있는 공장에서 현재의 생산능력 범위 내에서 최대의 이익을 창출 |
| 할 수 있는 A와 B의 생산량을 선형계획법으로 결정하고자 한다. 이 두 가지 제품은 ‘가’와 ‘나’의 공정 | |
| 을 거치는 데 순차적으로 거칠 필요는 없다. ‘가’와 ‘나’의 각 공정 에서의 소요시간과 각 공정의 | |
| 생산능력은 다음 표와 같고, 완제품의 판매이익은 A가 1,000원, B는 1,500원이다. | |
| (1) 이 자료를 바탕으로 최적해를 구하기 위한 선형계획 모형을 작성하시오. | |
| (2) 이 선형계획 모형으로 구한 해의 현실 적용 시 예상되는 문제점을 쓰시오. | |
 |
| 문) | A와 B의 2가지 제품을 생산하고 있는 공장에서 현재의 생산능력 범위 내에서 | ||
| 최대의 이익을 창출 할 수 있는 A와 B의 생산량을 선형계획법으로 결정하고자 | |||
| 한다. 이 두 가지 제품은 ‘가’와 ‘나’의 공정을 거치는 데 순차적으로 거칠 필요 | |||
| 는 없다. ‘가’와 ‘나’의 각 공정 에서의 소요시간과 각 공정의 생산능력은 다음 | |||
| 표와 같고, 완제품의 판매이익은 A가 1,000원, B는 1,500원이다. | |||
| (1) 이 자료를 바탕으로 최적해를 구하기 위한 선형계획 모형을 작성하시오. | |||
| (2) 이 선형계획 모형으로 구한 해의 현실 적용 시 예상되는 문제점을 쓰시오. | |||
 |
|||
| (1) 1. 의사결정변수 | |||
| A:A의 생산량 | |||
| B:B의 생산량 | |||
| 2. 목적함수 | |||
| Max Z = 1,000A + 1,500B | |||
| 3. 제약조건 | |||
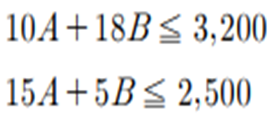 |
|||
| 4. | 비음조건 | ||
| 2쪽 | |||
| 번호 | |||
 |
|||
| 1. | 최적해 A= 131.81819, B=104.54545, Z= 288,636.365 | ||
| 2. | 현실 적용 시 문제점 | ||
| 공정별로 소요시간과 생산능력의 차이가 발생하고 있는 상태에서 최적해에 | |||
| 따라 생산을 계획할 경우 생산흐름의 불균형, 재공품의 과다, | |||
| 인력의 적정배치 등의 문제가 나타날 수 있다. | |||
| 12-97-3-3 | 신제품을 생산할 공장의 신설을 검토하고 있다. 신제품은 앞으로 10년간 계속 판매될 것으로 예상 |
| 되며 수요가 높을 확률은 60%, 낮을 확률은 40%로 예측되었다. 이러한 상황에서 공장규모를 대규모 | |
| 로 할 것인지, 소규모로 할 것인지의 전략을 결정하고자 한다. | |
| 시설투자를 대규모로 할 경우 2억 원, 소규모로 할 경우에는 1억 원이 필요하며, 시설물들에 대한 | |
| 10년 후 잔존가치는 없다. 수익은 대규모시설에서 수요가 높으면 10년간 매년 9,000만원, 대규모 | |
| 이나 수요가 낮으면 1,000만 원이다. 소규모시설 시 수요가 높으면 4,000만원, 수요가 낮으면 5,000 | |
| 만 원이다. 어떤 전략이 유리한지 결정하고자 할 때 디시전트리(Decision Tree)를 사용하여 작성하고, | |
| 기대수익을 계산한 후 유리한 전략을 선정하시오. |
| 문) | 신제품을 생산할 공장의 신설을 검토하고 있다. 신제품은 앞으로 10년간 계속 | ||
| 판매될 것으로 예상되며 수요가 높을 확률은 60%, 낮을 확률은 40%로 예측 | |||
| 되었다. 이러한 상황에서 공장규모를 대규모로 할 것인지, 소규모로 할 것인지 | |||
| 의 전략을 결정하고자 한다. 시설투자를 대규모로 할 경우 2억 원, 소규모로 | |||
| 할 경우에는 1억 원이 필요하며, 시설물들에 대한 10년 후 잔존가치는 없다. | |||
| 수익은 대규모시설에서 수요가 높으면 10년간 매년 9,000만원, 대규모이나 수 | |||
| 요가 낮으면 1,000만 원이다. 소규모시설 시 수요가 높으면 4,000만원, 수요가 | |||
| 낮으면 5,000만 원이다. 어떤 전략이 유리한지 결정하고자 할 때 디시전트리 | |||
| (Decision Tree)를 사용하여 작성하고, 기대수익을 계산한 후 유리한 전략을 | |||
| 선정하시오. | |||
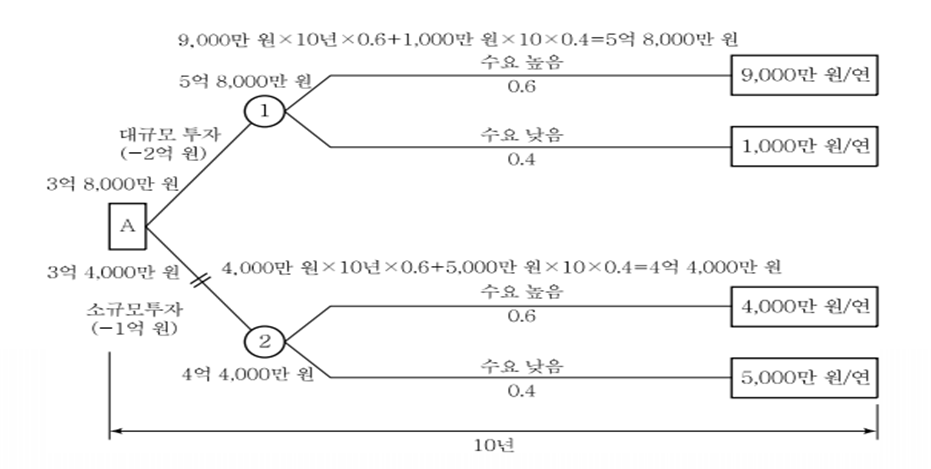
| 대규모 투자의 기대수익은 3억 8,000만 원이고, 소규모 투자는 3억 4,000만 원 | |||
| 으로 기대수익이 높은 대규모 투자 대안을 선정한다. | |||
 |
|||
| 12-97-3-5 | 대기행렬이론(Queueing Theory)에 대한 다음 각 물음에 답하시오. |
| (2) 대기행렬의 평균길이 |
| 문) | 대기행렬이론(Queueing Theory)에 대한 다음 각 물음에 답하시오. | ||
| (1) 대기행렬모형을 수리적으로 모형화하는 데 필요한 정보 4가지를 수리공장 | |||
| 의 예를 들어 설명하시오. | |||
| 있는 조건을 쓰시오. | |||
| (1) 1. 고객 | |||
| 1) 대상고객집단의 크기:무한 또는 유한으로 가정(무한표본 모집단으로 가정) | |||
| 2) 고객의 도착 패턴:일정한 분포 또는 확률분포로 가정(푸아송분포 가정) | |||
| 2. 서비스 시설 | |||
| 1) 서비스 시설의 구조:경로와 과정의 조합 | |||
| (1) 단일경로 단일과정 | |||
| (2) 단일경로 복수과정 | |||
| (3) 복수경로 단일과정 | |||
| (4) 복수경로 복수과정 | |||
| 3. 대기행렬 | |||
| 1) 대기행렬은 고객도착의 성격이나 서비스과정에 크게 의존하며 행렬의 길이 | |||
| 는 유한 또는 무한일 수도 있다.(지속적 대기행렬시스템으로 안정상태로 | |||
| 가정) | |||
| 2) 행렬의 규칙:FIFS, LIFS, GD(일반적 규정), SIRO(임의순) | |||
 |
|||
| 2쪽 | |||
| (2) | 1. 고객 도착은 푸아송분포 | ||
| 2. 서비스 시간은 지수분포 | |||
| 3. 단일경로 단일과정의 대기행렬시스템 | |||
728x90
반응형
'글쓰기' 카테고리의 다른 글
| 직업 심리학 2차 Sub-note 정리[31~45 ] (2) | 2024.10.03 |
|---|---|
| 공장관리기술사 기출 서브노트 -"10. 작업관리" (4) | 2024.10.03 |
| 공장관리기술사 기출 서브노트 -"23. SQC" (2) | 2024.09.10 |
| 용기의 아름다움, 관계의 힘 (0) | 2024.09.09 |
| 공장관리기술사 기출 서브노트 -"19. 설비보전" (5) | 2024.09.09 |